The following are true of the intersection of graphed equations:

• It can be a point (x, y) that occurs on both graphed equations.


• It represents a solution(s) that satisfies both equations.


• Not all pairs of graphed equations will have an intersection.


• Coinciding lines will have an infinite number of intersections.

Consider the two equations y = 4x and y = 2x + 6. The intersection of these two graphed equations represents a solution to both equations.

Follow the instructions below to further study examples of the intersection of graphed equations.

1. 1. Go to the Intersection of Graphed Equations Activity.


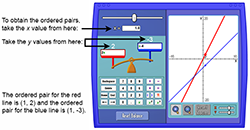
2. 2. Use this screen capture for instructions to obtain the ordered pairs.







3. 3. Enter 4x into the left side of the balance and 2x + 6 into the right side of the balance. Move the slider for x to zero. What do you notice?


4. 4. Move the slider for x to -3. What do you notice?


5. 5. Move the slider for x to 3. What do you notice?


6. 6. (3, 12) represents the intersection of the graphed equations y = 4x and y = 2x + 6.


7. 7. Repeat steps 1 to 6 using these two equations: y = 2x; y = x - 4


8. 8. Repeat steps 1 to 6 using these two equations: y = -2x - 1; y = x + 5


9. 9. Repeat steps 1 to 6 using these two equations: y = 2x + 4; y = 
   13
   x - 3

The ordered pair (2,4) is one solution to the equation y = 2x. The ordered pairs (3, 6), (4.5, 9), and (5.2, 10.4) are also solutions to the equation y = 2x.

y = 2x

4 = 2(2)

4 = 4