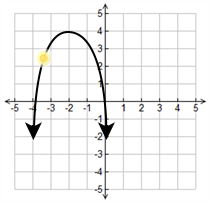
Vertex (algebraic)
My Definition
Key Characteristics
The following are true of a vertex (algebraic):
- The vertex can be a minimum or maximum point.
- For parabolas opening up or down, the x-value of the vertex is equidistant from the x values of the x-intercepts.
- For parabolas opening up or down, the y-value of the vertex is equidistant from the y value of the focus and the closest point on the directrix.
- For parabolas opening up or down, the x-value of the vertex is same as the x-value of all the points on the axis of symmetry.
- The x-value can be found using the formula h = -b2afor a parabola with the equation y = ax2 + bx + c.
- The y-value can be found by using the x-value into the equation, y = ax2 + bx + c, and simplifying.
- Similar statements can be made for parabolas opening to the left and right.
Example
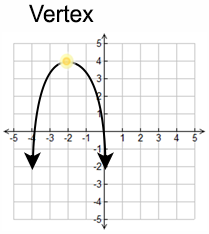
Non-example