
Algebra
Animal Systems
Lesson Preview
The animal science industry of agriculture is a labyrinth of information. One of the most common aspects among all parts of the animal science industry is the necessity for feeds and nutrition. This lesson will cover the various types of nutrients, their importance, and their role in animal nutrition. The difference between digestive systems will also be discussed, as well as calculating feed rations and costs using the Pearson Square and systems of linear equations.
TEKS Alignment
130.10.c.3B
Demonstrate knowledge of algebraic applications related to animal systems concepts such as ration calculation using the Pearson Square, percent homozygosity, heritability, USDA grade calculation, gene frequency, cost per unit of nutrient, and weaning weight ratio.
Lesson Objectives
Learner will . . .
Introduction
Proper nutrition is a vital aspect of animal health. A lack in the required nutritional elements for an individual can result in nutritional deficiency that may inhibit the body's immune response sytem, thus decreasing the ability to fight off infection. When considering pregnant animals, a situation such as this could cause birth defects or cause the female to abort the fetus(es). Nursing mothers could pass the deficiency and inhibited immune system to their young due to the lack of nutritional elements needed to provide the offspring with the diet they require to grow and develop properly. In geriatric animals, this could lead to death.
Livestock producers face many different aspects when considering nutrition and feeds. Nutritional requirements can change with the seasons, as well as the animal's stage of life. Another factor that must be considered is the time of the year and the feed stuffs that are available. For example, a Texas horse rancher would not be able to find fresh coastal hay very easily in the month of December. This will also have an impact on the cost of the feed - fresh coastal in December will be far more expensive than buying coastal hay in June since coastal's growing season is during the summer months. On the same token, sudan hay is an excellent hay for cattle, but would not be a good feed stuff for horses due to the high fiber content and the difference between the two species' digestive tracts.
Many producers have their feeds mixed using certain components they have chosen based on nutritional requirements. Current market prices for these components have an impact not only on the total price for the feed, but on the producer's decision to use the individual component as well. If a feed stuff was available, but extremely expensive at the given time, a less expensive component that is equal in nutrition could be substituted.
Overall, individuals that deal with livestock must continually check for updates with regard to their animals' nutrition requirements, available feeds, the costs involved with feeds and their components due to their constantly changing aspects.
Objective 1
Discuss the various nutrient requirements for livestock.
All animals require nutrients. However, all available nutrients and nutritional feed stuffs do not meet the needs of every animal. In other words, there is not one single feed that will meet the requirements of every individual animal. For example, the 2 year old Labrador that is constantly active will have different nutritional requirements than the 15 year old Quarter Horse brood mare. In order to know exactly what each animal needs, we must first consider the various types of nutrients and the role they play in nutrition as a whole.
There are 6 major classes of nutrients - water, protein, carbohydrates, fats, vitamins, and minerals.
Water
Protein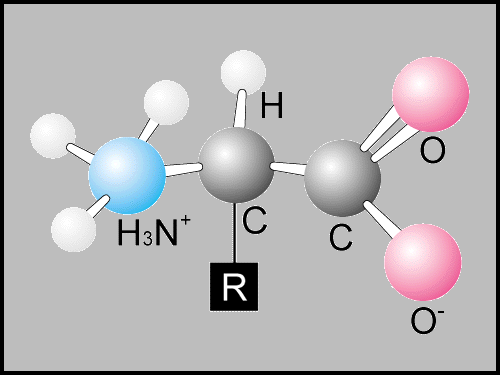
Carbohydrates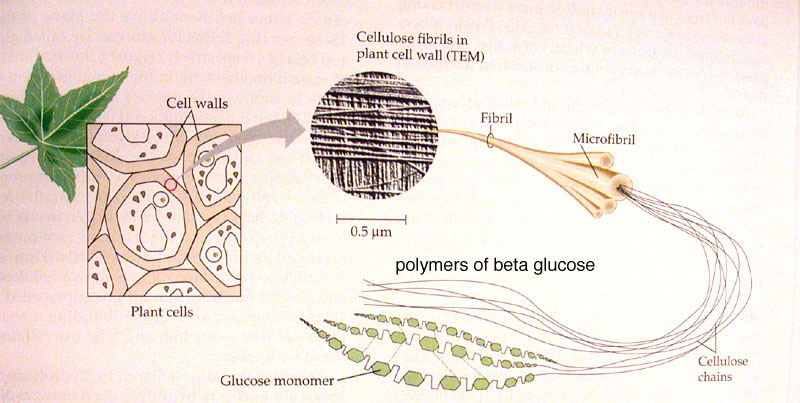
Fats
Vitamins


Minerals
Good nutrition can prevent many health issues with regard to animals. Poor nutrition often results in -
As animals grow, their nutritional needs change. Younger animals need diets higher in protein, while more mature animals require a diet higher in carbohydrates. Breeding animals' diets must meet the needs according to their production cycle.
|
Stage of Production |
Nutritional Requirements |
|
Delivery to Breeding |
Highest |
|
Breeding to Weaning |
Moderate |
|
Mid-Gestation |
Low |
|
Late Gestation |
High |

Nutritional requirements also vary according to the type of digestive system - monogastric or ruminant.
Monogastric stomachs, or simple stomachs, cannot digest large amounts of fiber, thus animals with this digestive tract will generally be fed concentrated feeds. The monogastric stomach secretes hydrochloric acid and enzymes to aid in breaking down feed into basic carbohydrates, proteins, and fats. Some of the smaller particles are absorbed by the body through the stomach wall. Horses and rabbits, however, contain a cecum, which allows these species to utilize high fiber feeds through microbial fermentation.
.jpg)
Ruminant digestive systems differ from monogastic systems in many ways. Where simple stomached animals have upper and lower incisor teeth, the ruminant animal only has teeth on the mandible. The maxilla is a dental pad that works with the lower incisors to tear off forages or other feed stuffs while grazing. Also, the ruminant animal will produce large amounts of enzyme packed saliva that will supply nutrients from the feed stuff to the microorganisms contained within the stomach.
Reticulum - the "hardware" stomach. This honeycomb shaped organ serves as the first stomach within the ruminant digestive system and traps indigestible objects (ie stones, wire, nails, etc.). It is also responsible for storing, sorting, and moving feed back up the esophogus for further digestion.
Rumen - the "storage vat" stomach. This giant stomach soaks, mixes, and ferments feed. Bacteria thrive in this stomach's environment and aid in the digestion of fiber and cellulose, as well as use nitrogen to form amino acids or protein. The bacteria contained within this stomach can also synthesize water soluble vitamins and vitamin K. As carbohydrates are broken down, fatty acids are released and absorbed through the rumen wall to provide the animal with energy. Young animals are not born with microorganisms, thus very little digestion occurs in the rumen.
Omasum - the "grinder" stomach. The third stomach of the ruminant system, the omasum is the location for the grinding of roughages and aiding in water absorption.
Abomasum - the "true" stomach. This stomach contains glands which excrete acids and contain enzymes that break down feeds, much in the same manner as a monogastric animal. Fiber that reaches this stomach has broken down to the point where it can be digested by the abomasum. In young ruminants, milk bypasses the first three stomachs by means of an esophageal groove.
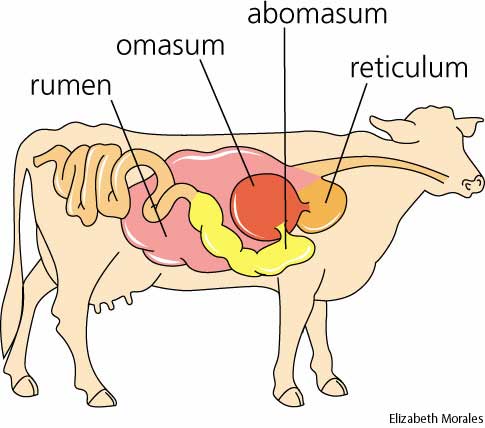
In both the monogastric and ruminant systems, there are organs that further break down and process nutrients. The pancreas secretes an enzyme to break down fat, while the liver secretes bile to digest fats and store iron. The small intestine serves as the final digestion and nutrient absorption organ. The large intestine's main functions are to absorb water and add mucous to the remaining material for easier passage through the remainder of the digestive tract.
Whenever choosing feeds for animals, it is highly important to provide materials that meet their nutritional needs. A monogastric animal will eat both plant and animal based feeds and will chew food before swallowing. Ruminants, however, primarily eat fibrous plant material and chews very little prior to swallowing. This results in the regurgitation of undigested feed later for more thorough chewing and digestion. Ruminants are fed diets high in fiber, such as course hays and straws, whereas monogastric animals can not break down this type of feed. Feeding a high fiber diet to a monogastric animal will cause other nutrients to be diluted and increase the rate that feed stuffs pass through the digestive system, thus allowing for less absorption time.
Many farmers and ranchers have their feeds custom made in order to insure that they are getting the materials they want to feed their animal. There are people in the industry who will calculate the ration with the requested feed stuffs to determine the amount of fat, protein, carbohydrates, digestibility, vitamins, minerals, etc. contained within the mixed contents. Depending on the current feed stuff prices, this can either save money or be more expensive when compared to a premixed feed.
Video: Fundamentals of Feed Mixing
Objective 2
Calculate feed rations for given species.
When calculating feed rations, the most often used tool is the Pearson Square. It shows the proportions or percentages of 2 feeds that will be mixed together, as well as a percentage of the needed nutrients. Feeds for rations should be selected according to the animal's nutritional needs, the price of the components being used, the availability of the feed, and the desirable nutrients found in the materials.
EXAMPLE - Part 1
Joe Showmaker has purchased his barrow recently for the State Fair show. The current weight of his pig is 50 pounds, but he will need to weigh 250 pounds by the weigh-in at the fair. If pigs have an industry average feed conversion ratio of 3.5, how many pounds of feed is it going to take to raise Joe's pig to 250 pounds?
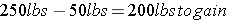
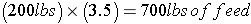
Part 2
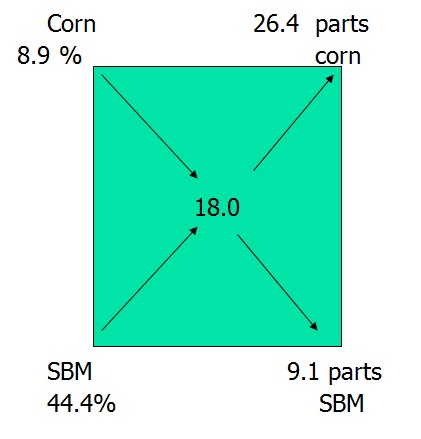
A feeding standards table shows that an 18% crude protein ration is needed. If Corn (8.9% crude protein) and Soybean Meal (44.4% crude protein) are chosen as feeds. Use the Pearson Square to calculate how much of each component will be needed to make the required 700 pounds of feed while achieving the 18% crude protein.
Step 1: Draw a square with diagonal lines across the square. 
Step 2: Write the percentage of crude protein needed by the animal in the center of the square where the diagonal lines cross. 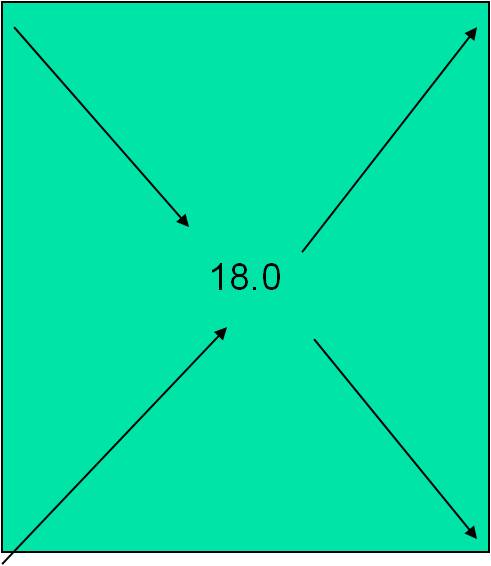
(NOTE: The specific crude protein needed by species would come from a feed chart.)
Step 3: Write the components to be used at each corner. ALWAYS place the primary feed in the bottom left corner.Be sure to place the percent of crude protein after the name of the feed.
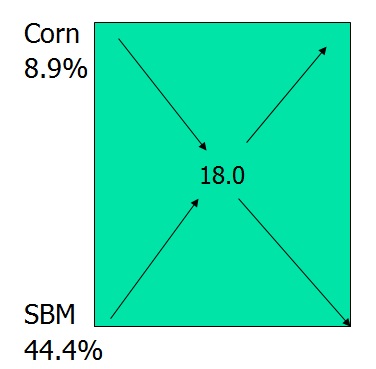
Step 4: Take the protein level of each feed ingredient and subtract it from the amount of protein needed in the center of the box. Then, record the answer in the opposite corner.
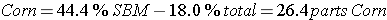
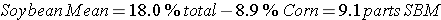
NOTE: We never want a negative value when dealing with feed rations. Always subtract the lower crude protein percentage from the higher percentage.
Step 5: Calculate the percentage of each component needed in the ration.
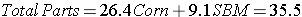
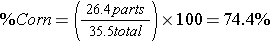
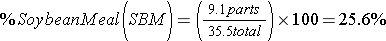 OR
OR 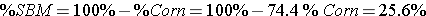
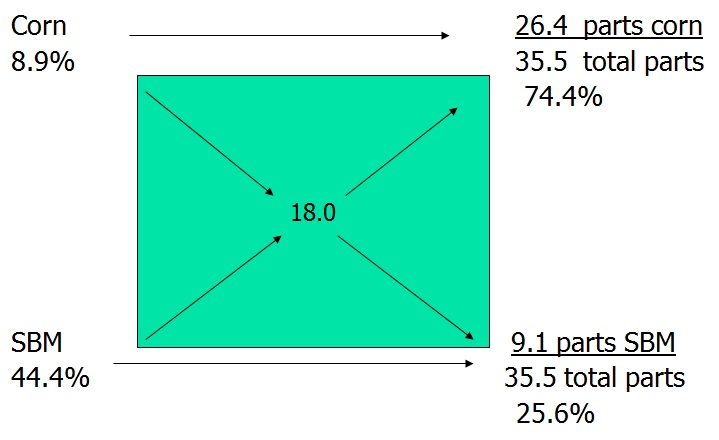
Step 6: To find the amount of each component needed for a specific weight (ie 700 pounds), multiply the percentage of each component by the amount of feed desired.
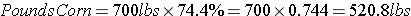
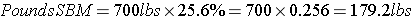 OR
OR 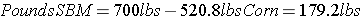

Video: Utilizing The Square Method to Balance Rations
Objective 3
Evaluate the cost of the rations using current market prices.
Market prices change dramatically over time, especially during this economic roller coaster. According to the commodities market as of June 27, 2011, Corn prices closed at 626.75 cents per bushel for a December 2011 delivery. With bushels of corn weighing 56 pounds per bushel, that calculates out at -
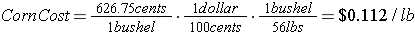
From our Pearson Square calculations above, our barrow would need 520.8 pounds of corn to mix with soybean meal for his rations. If we were purchasing corn at this price, prior to tax, etc., the total cost would calculate to -
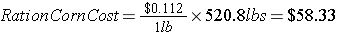
Unfortunately, the price for corn had dropped 0.83% since the market closing on June 26, 2011. Even more unsettling for Joe Showmaker is the 2.99% drop in lean hog prices - 92.35 cents per pound for an August 2011 contract.
If Joe paid the current corn prices, and soybean meal is valued at 340.7 cents per bushel for a December delivery, his feed ration would calculate out as follows.
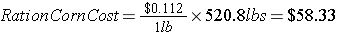
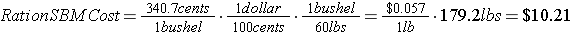
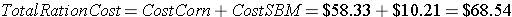
If Joe paid $200 for his show barrow, fed him to show weight, then sold his barrow at the current lean hog price, his approximate earnings would calculate to -
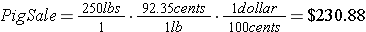
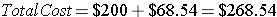
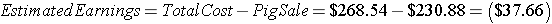
Using current commodity prices, Joe will actually be losing money on his show barrow project. If he had paid more for his barrow, which is common in the livestock show industry, he would have lost even more money in the venture. On the other hand, if lean hog prices change for the better and close at a higher rate when the barrow is at show, he could turn a profit. When dealing with grains, feeds, or any other market commodity where the value changes daily, it is best to watch the market and lock in contracts when the futures value is at a peak.
Video: 40+ year trading veteran sees multi-year bull market in agriculture...but not for the "dumb" money
Objective 4
Understand various ways of solving systems of equations, including substitution and elimination.
Solving for feed rations can also be done algebraically through the process of solving systems of linear equations. Systems of linear equations are used to find the value of more than one variable at a time (e.g. the amount of different types of feed). A linear system of equations consists of more than one linear equation. A linear system of equations may be solved when there is the same number of equations as variables. For instance, if there are two variables, x and y, and two equations, then the system is solvable. Solving systems of equations involves finding solutions for the variables that will simultaneously satisfy all equations in the system. A system of linear equations may be solved using various methods, such as substitution, elimination, graphing, gaussian elimination, or using inverses of matrices. This section focuses on solving systems of equations using either the method of substitution or elimination.
Method of Substitution:
Step 1: Solve one of the equations for one of the unknowns. Choose the equation that is easiest to solve for a variable. Typically, this would be the equation that has a variable whose coefficient is 1 or - 1.
Step 2: Substitute the expression that equals the variable solved for in Step 1 into the other equation. The result will be a single linear equation in one unknown.
Step 3: Solve the linear equation found in Step 2.
Step 4: Substitute the value of the variable into the expression found in Step 1 to find the value of the other variable.
Step 5: Check your answer.
(Sullivan & Struve, 2009)
Example1: Solve the following systems of equations by the method of substitution: 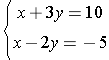
Solution:
Step 1: Solve for x in equation 1.
x + 3y = 10
x + 3y - 3y = 10 - 3y Subtract 3y from both sides to isolate x.
x = 10 - 3y
Step 2: Substitute 10 - 3y for x in equation 2.
x - 2y = -5
(10 - 3y) - 2y = -5
Step 3: Solve for y.
10 - 3y - 2y = -5 Drop parenthesis
10 - 5y = -5 Combine like terms
10 - 10 - 5y = -5 - 10 Subtract 10 from both sides
-5y = -15
-5y/-5 = -15/-5 Divide both sides by -5
y = 3
Step 4: Substitute 3 for y in the equation found in step 1.
x = 10 - 3y
x = 10 - 3(3)
x = 10 - 9
x = 1
Step 5: Check x=1 and y=3 by plugging them into the two original equations.
x + 3y = 10
1 + 3(3) = 10
10 = 10
x - 2y = -5
1 - 2(3) = -5
-5 = -5
Therefore (1,3) is the solution to the systems of equations.
Method of Elimination:
Step 1: Multiply both sides of one or both equations by a nonzero constant so that the coefficients of one of the variables are additive inverses.
Step 2: Add equations (1) and (2) to eliminate the variable whose coefficients are now additive inverses. Solve the resulting equation for the unknown.
Step 3: Back-substitute the value of the variable found in Step 2 into one of the original equations to find the value of the remaining variable.
Step 4: Check your answer.
(Sullivan & Struve, 2009)
Example 2: Solve the following system of equations by elimination: 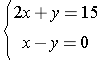 .
.
Solution:
Step 1: When choosing a variable to eliminate, the goal is to make the variable have the same coefficients but opposite in sign. Therefore in this problem we will choose to eliminate y since the coefficients of y are the same but opposite in sign. Hence, in this problem, there is no need to multiply both sides of one or both of the equations by a nonzero constant. Note that x could have been eliminated instead of y, and you will arrive at the same solution.
Step 2: 2x + y = 15
+ x - y = 0
3x = 15
3x/3 = 15/3 Divide both sides by 3
x = 5
Step 3: Substitute 5 for x in equation 2 and solve for y.
x - y = 0
5 - y = 0
5 - 5 - y = 0 - 5 Subtract 5 from both sides
-y = -5
-y/-1 = -5/-1 Divide both sides by -1
y = 5
Step 4: Check x=5 and y=5 by substituting them into the original equations.
2x + y = 15
2(5) + 5 = 15
10 + 5 = 15
15 = 15
x - y = 0
5 - 5 = 0
0 = 0
Therefore the solution to the system of equations is (5,5).
When solving a system of linear equations, there are three possible solutions. Since the system involves two lines, then there are three options for the two lines:
1) The two lines may intersect in one point, which in this case there is one solution to the system of equations. This type of system is known as a consistent independent system. Examples one and two are consistent independent systems.
2) The two lines may be parallel and never intersect, in this case there are no solutions to the system of equations. This type of system is known as an inconsistent system.
3) The two lines are the exact same line and lie on top of each other. In this case there are infinitely many solutions to the system of equations. This type of system is known as a consistent dependent system.
Example 3: Solve the following system of equations: 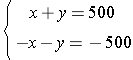
Solution: Solving by elimination may be the easier of the two methods here.
Step 1:Notice that the coefficients of x are the same but different in sign, and so are the coefficients of y. Therefore, there is no need to multiply either of the two equations.
Step 2: x + y = 500
+ -x - y = -500
0x + 0y = 0
0 = 0
Since both of the variables eliminated, then the system is either a consistent dependent system or an inconsistent system. If the last statement after elimination is a true statement, then the system is a consistent dependent system. If the last equation is false, then the system is inconsistent. Hence, in this example the last statement is true and thus the system is a consistent dependent system, meaning there are infinitely many solutions to the system.
Example 4: Solve the following system of equations: 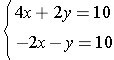 .
.
Solution: Solve by eliminating y.
Step 1: In order to make the coefficients of y the same, but opposite in sign we must multiply equation 2 by 2.
4x + 2y = 10 -› 4x + 2y = 10
2(-2x - y = 10) -› -4x - 2y = 20
Step 2: Add the two equations together.
4x + 2y = 10
+ -4x - 2y = 20
0 = 30
Since both variables were eliminated and the last statement is false, then the system is inconsistent, meaning there are no solutions to the system of equations.
Let's Practice:

Objective 5
Solve systems of linear equations in the context of animal systems.
In this section, we provide a particular example in animal systems in which a system of equations can be used to find solutions. Other examples of situations in animal systems are also presented in the quiz group in this section.
Example: A feed store sells grain mixtures for horse feed. If cracked corn sells for 10 cents per kilogram and crimped oats sell for 12 cents per kilogram, what amount of corn and oats should be mixed so that a 30-kilogram bag of the mixture would sell for $3.00?
Solution:
Step 1: Identify what you want to know, and label the unknowns.
We want to know how many kilograms of cracked corn and how many kilograms of crimped oats. Let x represent the kilograms of corn and y represent the kilograms of oats.
Step 2: Represent the data in a table.
|
|
Price per kg |
Number of kgs |
Cost |
|
$0.10 corn |
0.10 |
x |
0.10x |
|
$0.12 oats |
0.12 |
y |
0.12y |
|
mix |
0.10 ($3.00/30) |
30 |
3.00 |
Step 3: Set up two equations, one representing cost, and the other representing the number of kilograms.
Cost: 0.10x + 0.12y = 3.00
Amount: x + y = 30
Step 4: Solve the system of equations.
Solve by substitution.
Step 1: x + y = 30
x + y - y = 30 - y Subtract y from both sides to solve for x.
x = 30 - y
Step 2: 0.10x + 0.12y = 3.00
0.10(30-y) + 0.12y = 3.00 Distribute
3 - 0.10y + 0.12y = 3.00
3 + 0.02y = 3.00 Combine like terms
3 - 3 + 0.02y = 3-3 Subtract 3 from both sides
0.02y = 0
0.02y/0.02 = 0/0.02 Divide both sides by 0.02
y = 0
Step 3: x = 30 - y
x = 30 - 0
x = 30
Step 4: 0.10(30) + 0.12(0) = 3.00
3 + 0 = 3
3 = 3
x + y = 30
30 + 0 = 30
30 = 30
Therefore 30 kilograms of corn and 0 kilograms of oats should be mixed.
These types of mixture problems can also be solved using The Pearson Square, which we choose not to focus on in this lesson. For more information on the Pearson Square method you may refer to the following reference:
Rogers, C. C. (2000). Mathematics for agriculture. Danville, IL: Interstate Publishers.
Lets Practice:

Problem Activity
Tyler Mann has just purchased 600 broilers to raise for the upcoming show season. He wishes to mix his own feed, using the information below.
1. How many pounds will the broilers need to gain before the show?
2. What is the total amount of feed that will be needed per bird? All 600 birds?
3. Calculate the feed ration for the given feed stuffs. What percentage of the total feed should be made up of Corn? Cotton Seed Meal?
4. What is the total amount of corn and cotton seed meal that will be needed for the mixture (in pounds)?
5. If the current price of corn is 694.0 cents per bushel, and cotton seed meal is 265.0 cents per ton, how much will each cost for the mixture? NOTE: 1 bushel of corn weighs 56 pounds.
Best Practices
Suggestions:
1. Take students to local feed stores with the task of purchasing two types of feed. Give each student a certain amount of pounds to purchase and an amount that needs to be spent. Have students find the feed and determine the amount of each feed needed to be purchased. You may use the following activity sheet to help with this activity. Feel free to make any changes to accomodate your trip to the local feed store.
Feed Store Activity Sheet
2. Perform a feed mixing lab with students using edible items, such as cereals and candy that are labeled as something else. Such a lab can be found at http://naae.ca.uky.edu:8080/clearspace_community/docs/DOC-2546.
Additional Resources
Websites:
www.sosmath.com/soe/SE/SE.html
www.ehow.com/how_4845885_system-solution-infinitely-many-solutions.html
http://ohioline.osu.edu/b762/b762_15.html
http://www.ers.usda.gov/data/feedgrains/Documentation.aspx
http://www.isd743.k12.mn.us/AgTableofContents.htm
Videos:
Solving Systems of Equations via Substitution
Algebra 1 Solving Systems of Equations using Elimination with Multiplication
Graphing Systems of Equations
References
Bates, A. (2011). CTE Online Lesson Plan. From Food to Feces: Monogastric vs. Ruminant.
Derington, J. (2011). Livestock Production course notes.
Rockswold, G. (2010). College algebra with modeling and visualization. Boston, MA: Addison-Wesley.
Rogers, C. C. (2000). Mathematics for agriculture. Danville, IL: Interstate Publishers.
Sullivan, M., & Struve, K. R.. (2009). Intermediate Algebra. New Jersey: Prentice Hall.
Websites:
www.colostate.edu
www.money.cnn/data/commodities
www.agriculture.com/markets/commodities
http://www.yourdictionary.com/abomasum
http://www.seminolewellnessfeed.com/WellnessEquineNutrition.htm