Center of Dilation
My Definition
Key Characteristics
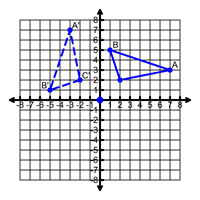
The following are true of the center of dilation:
- On a coordinate plane, the center of dilation can be any point, but the origin is commonly used.
- The ratio of the distance from the center of dilation to any point on the image compared to the distance from the center of dilation to the corresponding point on the pre-image will result in the scale factor, k.
- Lines drawn through each point on the pre-image and its corresponding image point will intersect at the center of dilation.
- When the origin is the center of dilation, each point on the pre-image (x,y) corresponds to (kx, ky) on the image.
Example
Click on the link below to see an example of the center of dilation.
Center of Dilation Activity
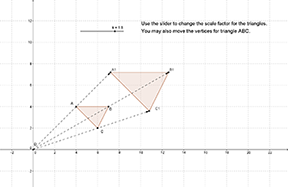
Non-example
The point (0, 0) is the center of rotation for the transformation below.