When you are asked to “solve a quadratic equation,” there are many ways to find the solutions. What you are really looking for are the ROOTS of the function. Just like the roots of a plant holding it stationary in the earth, the REAL ROOTS of a quadratic function are where the parabolic graph is attached to the x-axis. If you are looking at the graph of a quadratic function, you can see where the parabola is crossing the x-axis and find the real roots since they are crossing a real number line (the x-axis).
For example #1, look at the graph below and move your mouse over the ROOTS of the function. We are looking for where the function input (domain) produces a ZERO output or range value.
The parabola is the graphical representation of the equation y = one-half 1 2 x2 − 2x − 6
Can you see that the parabola is crossing the x-axis in two places? At x= -2 and again where x = 6. Do you think all roots of quadratics cross the x axis in a NICE integral place? Just like we can’t all live at an easy-to-find location, the graph of a parabola will not always cross the x axis with simple integral locations. You will use other functions on your graphing calculator, or other strategies, to find the solution(s), or roots. You can also assume that not all quadratic functions have two roots. Sometimes the parabola kisses the x-axis, as you see in example #2 below:
(move your mouse over the ROOTS of the function)
However, some quadratic functions have NO REAL ROOTS at all, as seen below in example #3:
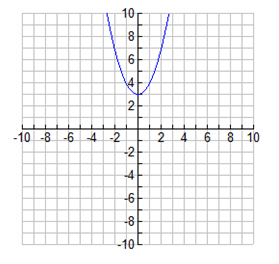
Since the graph does not cross the x-axis, the solution(s) to the function are found by using the quadratic formula and are imaginary roots.
When learning about roots of quadratics, the graphical values are usually demonstrated first so the solution(s) or roots are easier to comprehend.
Another strategy used to solve a quadratic equation involves factoring.
The equation of the graph in example #1 above can be reformatted in factored form as:
.5(x + 2) (x – 6)
Note that if x equals -2 or 6, then y = 0 since one of the variable binomial factors would become equal to 0 and produce a 0 product for y. Here the understanding of how a PRODUCT can be zero is important.