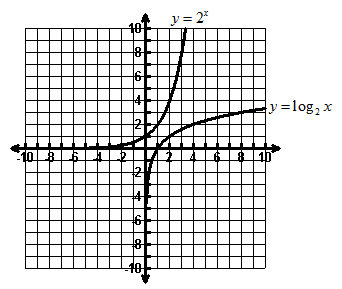
A logarithmic function is the inverse of an exponential function.
Given the graph of the exponential function, y = 2x, the inverse of the function is y = log2x.

| y = 2x | |
| x–intercept | none |
| y–intercept | (0, 1) |
| Horizontal asymptote | y = 0 |
| Vertical asymptote | none |
| Domain | All real numbers |
| Range | {y | y > 0} |
| Point on graph | (1, 2) |
| y = log2 x | |
| x–intercept | (0, 1) |
| y–intercept | none |
| Horizontal asymptote | none |
| Vertical asymptote | x = 0 |
| Domain | {x | x > 0} |
| Range | All real numbers |
| Point on graph | (2, 1) |
In your notes, record four similarities you found in looking at the properties of the two functions.
