Confidence Intervals and two independent sample means

Consider the situation where you want to know if there is a significant difference in the means of two independent samples (For instance, what is the difference in the mean ages of mothers in two different countries when they give birth to their first child?). It is important that the two samples are obtained independently of each other in order for the following confidence interval to be valid.

As in the previous lesson, we won't know the standard deviation of either population, so we will have to use the sample standard deviations as our best estimate. Thus, the formula for the standard error of the difference of the two means is given by the formula:

 

 

 

Once you have calculated SE_D you will need to compute the margin of error. Just as before, the margin of error is made up of two parts:

The critical t value will have approximately 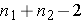degrees of freedom (note that computer software that calculates the margin of error will use a more precise, but more complicated method of determining the degrees of freedom).

Finally, you are ready to construct the confidence interval:

Lower Limit = point estimate - margin of error

Upper Limit = point estimate + margin of error

 

Where the point estimate is the difference in the mean . The order you choose to subtract to produce the difference doesn't matter - either order will produce a valid confidence interval. Assuming the two means are of different values, one subtraction order will produce a positive difference and the other order a negative difference. Depending on the context of the situation you may find the positive difference to be easier to interpret.

 Using the following data set, compute a 95% confidence interval.

 

First you will need to compute the mean and standard deviation for each group.

Next you will compute the difference in the group means and the standard error of the difference.

 

For the critical t value, note the degrees of freedom are 10 + 10 - 2 = 18 and from a table of critical t values, for 18 degrees of freedom the critical t value is 2.101. Now you have everything you need to compute the margin of error and the limits of the confidence interval.

 

 

PRACTICE PROBLEM #3

You try one! A researcher selects a pair of random samples. In Group 1 the scores are 20, 14, 16, 18, 16, 15, 14. In Group 2 the scores are 23, 20, 21, 24, 18, 22, 24. Find the 99% Confidence Interval.

 

ANSWER

 

 

return to top | previous page | next page