Confidence Intervals
Statistics & Risk Management
Confidence Intervals
Statistics & Risk Management
A candidate in a two-person election commissions a poll to determine who is ahead. The pollster randomly chooses 500 registered voters and determines that 260 out of the 500 favor the candidate. In other words, 0.52 (p) of the sample favors the candidate. Although this point estimate of the proportion is informative, it is important to also compute a confidence interval to account for the variation in p that would result from different samples. The confidence interval is computed based on the mean and standard deviation of the sampling distribution of a proportion. The formulas for these two parameters are shown below.
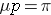
The form of the confidence interval remains the same as before
Then the limits of the confidence interval are also calculated as before:
Since we do not know the population parameter π, we use the sample proportion p as an estimate. The estimated standard error of p is therefore
We start by taking our statistic (p) and creating an interval that ranges (Zc) in both directions. The value of Zc is found in the table as normal (1.96). However, unlike our other confidence intervals, we must make a slight adjustment to correct for the fact that the distribution is discrete rather than continuous.
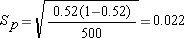
To correct for the fact that we are approximating a discrete distribution with a continuous distribution (the normal distribution), we subtract 0.5/N from the lower limit and add 0.5/N to the upper limit of the interval (Note: the continuity correction is not used by many people and may be omitted with little difference in the limits of the interval). Therefore the confidence interval is
Based on these calculations, we can be 95% confident that the true proportion of voters who favor the candidate is somewhere between 0.475 and 0.565
Since the interval extends 0.045 in both directions, the margin of error is 0.045. In terms of percent, between 47.5% and 56.5% of the voters favor the candidate and the margin of error is 4.5%. Keep in mind that the margin of error of 4.5% is the margin of error for the percent favoring the candidate and not the margin of error for the difference between the percent favoring the candidate and the percent favoring the opponent. The margin of error for differences is 9%, twice the margin of error for the individual percent. Keep this in mind when you hear reports in the media; the media often get this wrong.
PRACTICE PROBLEM #4
Now you try! A candidate in a two-person election commissions a poll to determine who is ahead. The pollster randomly chooses 1000 registered voters and determines that 300 out of the 1000 favor the candidate. Compute the 95% confidence interval.
Created with SoftChalk
mobile page
