
Organizing and Describing Data
Statistics & Risk Management
Descriptive statistics are numbers that are used to summarize and describe data. The word "data" refers to the information that has been collected from an experiment, a survey, a historical record, etc. If we are analyzing birth certificates, for example, a descriptive statistic might be the percentage of certificates issued in New York State, or the average age of the mother. Any other number we choose to compute also counts as a descriptive statistic for the data from which the statistic is computed.
Several descriptive statistics are often used at one time, to give a full picture of the data. We decide which descriptive statistic is appropriate based on the shape of the curve and/or the nature of the distribution.
Measures of Central Tendency
With tables and graphs we have a picture of the distribution of our data. Now we will look at some numerical ways to summarize them. The key to summarizing you data lies with the central tendency . A measure of central tendency is a calculated value that is typical of the entire distribution. There are three primary measures of central tendency:
. A measure of central tendency is a calculated value that is typical of the entire distribution. There are three primary measures of central tendency:
A. Mean =
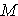

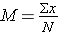

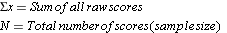

 distribution
distributionExample 1:
|
Data point |
X |
|
1 |
10 |
|
2 |
11 |
|
3 |
15 |
|
4 |
12 |
|
5 |
16 |
|
N = 5 |
∑x = 64 |

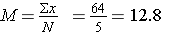
PRACTICE PROBLEM 1.3:
Find the mean of the following data set
|
9, 8, 3, 7, 9, 7, 9, 5, 8, 5, 4, 6, 6, 7, 5, 3, 2, 8, 5, 8, 8, 8, 4 |
ANSWER 1.3 (Mouse-Over to Check Your Answer).
B. Median = 
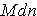

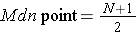
From the low value, count this many places to find the Mdn value.
Example 2:
|
Data point |
x |
|
1 |
10 |
|
2 |
11 |
|
3 |
12 |
|
4 |
15 |
|
5 |
16 |
|
N = 5 |
∑x = 64 |

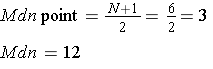
Example 3:
|
Data point |
x |
|
1 |
10 |
|
2 |
11 |
|
3 |
12 |
|
4 |
15 |
|
5 |
16 |
|
6 |
17 |
|
N = 5 |
∑x = 64 |

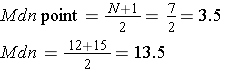
PRACTICE PROBLEM 1.4:
Find the Median of the following data set.
|
9, 8, 3, 7, 9, 7, 9, 5, 8, 5, 4, 6, 6, 7, 5, 3, 2, 8, 5, 8, 8, 8, 4 |
C. Mode =
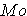
PRACTICE PROBLEM 1.5:
Find the Mode of the following data set
|
9, 8, 3, 7, 9, 7, 9, 5, 8, 5, 4, 6, 6, 7, 5, 3, 2, 8, 5, 8, 8, 8, 4 |
Measures of Variability
What is variability? Variability is a measure of dispersion; the degree to which individual scores in a data set differ from one another. It is another set of descriptive statistics.
A. Range =
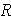
Example 4:
Exam scores for two different courses:
| Class A | Class B |
| 78 | 82 |
| 82 | 90 |
| 95 | 91 |
| 100 | 79 |
| 65 | 78 |
 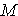 = 84 = 84 |
 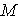 = 84 = 84 |
 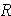 = 35 = 35 |
 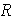 = 13 = 13 |
B. Standard Deviation
1. Population Standard Deviation =
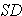 or
or 
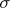

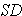 or
or 
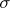 represents the population standard deviation
represents the population standard deviation
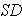

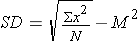


1) Set up the following table and take the sum of all raw scores (∑X).
|
Data point |
X |
|
1 |
10 |
|
2 |
11 |
|
3 |
12 |
|
4 |
15 |
|
5 |
16 |
|
6 |
20 |
|
7 |
13 |
|
8 |
15 |
|
9 |
17 |
|
10 |
19 |
|
N = 10 |
∑x = 148 |
2) Add another column made of the square of each X, taking the sum of this column (∑X2).
|
Data point |
X |
X2 |
|
1 |
10 |
100 |
|
2 |
11 |
121 |
|
3 |
12 |
144 |
|
4 |
15 |
225 |
|
5 |
16 |
256 |
|
6 |
20 |
400 |
|
7 |
13 |
169 |
|
8 |
15 |
225 |
|
9 |
17 |
289 |
|
10 |
19 |
361 |
|
N = 10 |
∑x = 148 |
∑x2 = 2290 |
3) Find the Mean.

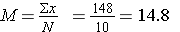
4) Use the collected sum'd data in the formula:

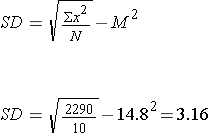
PRACTICE PROBLEM 1.6:
The following data set represents a population of scores. Find the SD.
|
10, 6, 11, 15, 18, 20, 17, 12, 10, 9, 19, 16, 14, 11, 10, 21, 22 |
2. Estimated Standard Deviation =
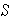

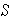

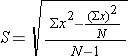

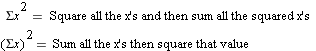
NOTE the differences between 
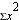 and
and 
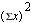
1) Set up the following table and take the sum of all raw scores (∑X)
|
Data point |
X |
|
1 |
10 |
|
2 |
11 |
|
3 |
12 |
|
4 |
15 |
|
5 |
16 |
|
6 |
20 |
|
7 |
13 |
|
8 |
15 |
|
9 |
17 |
|
10 |
19 |
|
N = 10 |
∑x = 148 |
2) Add another column made of the square of each X, taking the sum of this column (∑X2)
|
Data point |
X |
X2 |
|
1 |
10 |
100 |
|
2 |
11 |
121 |
|
3 |
12 |
144 |
|
4 |
15 |
225 |
|
5 |
16 |
256 |
|
6 |
20 |
400 |
|
7 |
13 |
169 |
|
8 |
15 |
225 |
|
9 |
17 |
289 |
|
10 |
19 |
361 |
|
N = 10 |
∑x = 148 |
∑x2 = 2290 |
3) Use the collected sum'd data in the formula:

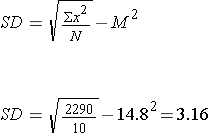
PRACTICE PROBLEM 1.7:
The following data set represents a sample of scores. Find the S
|
10, 6, 11, 15, 18, 20, 17, 12, 10, 9, 19, 16, 14, 11, 10, 21, 22 |
3. Variance =
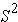
PRACTICE PROBLEM 1.8:
The following data set represents a sample of scores. Find the S²
|
10, 6, 11, 15, 18, 20, 17, 12, 10, 9, 19, 16, 14, 11, 10, 21, 22 |
Take a moment to compare the three formulas. Make sure you understand the difference among the 3.
Descriptive statistics are just descriptive.They do not involve generalizing beyond the data at hand. Generalizing from our data to another set of cases is the business of inferential statistics.
It is not practical to ask every single American how he or she feels about the fairness of the voting procedures. Instead, we query a relatively small number of Americans, the sample , and draw inferences about the entire country, the population, from their responses. The Americans actually queried constitute our sample of the larger population of all Americans. This is inferential statistics.
, and draw inferences about the entire country, the population, from their responses. The Americans actually queried constitute our sample of the larger population of all Americans. This is inferential statistics.
Since we are inferring the characteristics of a large body of possible observations from a smaller select group of observations, it is crucial that it be representative. In looking at our sample of Americans, for it to be representative, it must not over represent one kind of citizen at the expense of others. For example, something would be wrong with our sample if it happened to be made up entirely of Florida residents. If the sample held only Floridians, it could not be used to infer the attitudes of other Americans. The same problem would arise if the sample were comprised only of Republicans. Inferential statistics are based on the assumption that sampling is random. We trust a random sample to represent different segments of society in close approximation to the actual population proportions.