Populations and Samples, Parameters and Statistics
Have you put any thought into how you would determine the average height of the American male? You could always attempt to measure "every single adult male in America". The total number of American males would then become our population. If we were able to, we would find the mean (
) and standard deviation (
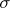) (Remember that there is a difference between the population's standard deviation and estimates of the standard deviation: refer back to the Measures of Variability in module one). These measurements ( 
and 
) would be called parameters.
But is this really possible? Could we actually measure every American male? If you think so, I am sure there are many census takers out there who would disagree.
Instead of attempting to measure all American males, you could take a small group of American males and measure them. In fact, this second option is what we would do. This would represent our sample.
So we are going to take a sample of n American males and record the height of each (x). Then we can compute the sample mean (M) and the sample standard deviations (s).
However, the question still remains. How do we assume that we know the average height of all American males after the measurements of a small group of American males? For this to work, we have to have a random sample. If we have representativeness with our sample, then our sample will estimate the whole population, but this is not as easy as it sounds. To be truly representative, every individual in a population must have equal likelihood of being selected for the sample. Also, remember the law of large numbers. Representativeness is also based on probability. And we know from the previous lesson on probability that our observations only become close to our expected outcomes with large numbers. So in other words, the chance that 10 people accurately represent all Americans is very low. One thousand Americans in a sample? Much more likely.
Going back to our early Egyptian/Citron example. Do you think the Egyptian Magistrate's group of criminals was a representative sample? Why or why not?
